Modeling Contagion with Markov Chains

Is it rational to quarantine sick kids? typo

My children’s day care has a strict policy of sending kids home who have runny noses. The fear is that the potential cold will spread to the other kids. Is it rational to have such a strict policy? I decided to try modeling the problem as a simple two-stage Markov process.

The first step is to create the transition matrix. The transition matrix gives the probabilities that the contagion spreads (or decreases) among the (n=6) children.

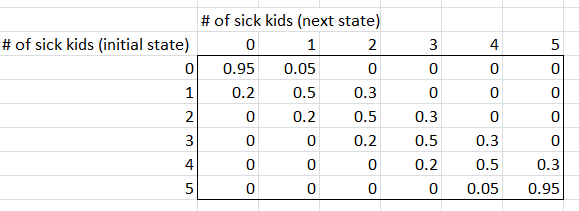
The assumptions behind transition probabilities are as follows:

1. If there are no sick kids, there is a 95% chance that there will be no sick kids the next day, and a 5% chance there will be one sick kid.
2. If there are n sick kids, there is a 50% chance the contagion doesn’t spread. There is a 30% chance that another child is infected, and a 20% chance that one child is no longer infected (such as by staying home and recovering).
3. If all n of the kids are sick, there is a 95% chance that they all stay sick, and a 5% chance that one kid recovers.

A couple of caveats on these transition probabilities. First, I would describe the probabilities as linear- the infection only spreads one child in a given step. That is, there is 0 probability that, for example, if there are 2 infected kids, there will be 4 infected kids the next day. Second, to add some risk of complete contagion, I assume that if all the kids are infected, they’re 95% likely to all stay infected. Both of these caveats can be addressed in a more complex model.

I used the R package markovchain to quickly model the spread of the contagion. One nice thing about this package is that you can quickly visualize the Markov chain, below.

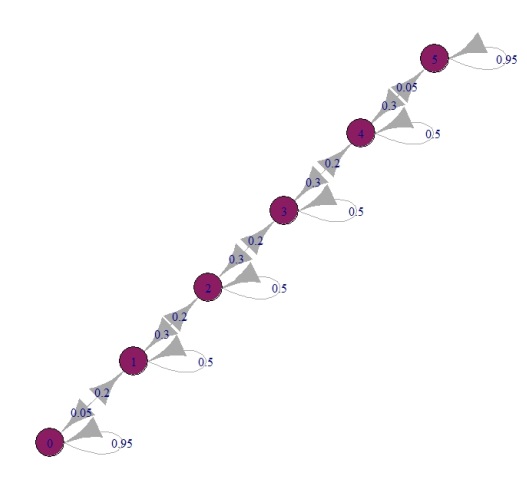
The red circles represent the number of sick kids in a given step.

So, is it rational to have a super strict sick policy? To answer this question, I modeled two different scenarios.

First, assuming an initial state of one sick child, how many sick children would there be after four days? The model estimates a 15% chance that there will be at least one sick child.

Second, again assuming an initial state of one sick child, how many sick kids will there be in the long run? This is where things get scary. There is only a 12% chance that the contagion will be eradicated, and a 63% chance that all of the kids will be infected.

In conclusion, the concern is not that everything is going to go haywire, but that it will be difficult to eradicate the contagion entirely. I can understand this, and I think it validates the strict policy.